Finding the beam theory papers was just a baby step to designing my own bars. What I needed was software to apply the math. It may have been possible to write the software from the math in the papers, but software like that can be very difficult to write and debug, especially given my very tenuous grasp on the mechanical engineering concepts that underlie it. My breakthrough moment was when I found a masters thesis on the web that was written by Mingming Zhao. The paper, called “Automatic multi-modal tuning of idiophone bars,” utilized the standard beam theory to compute the bar shapes, but most importantly, the appendix contained the actual Matlab code that applied the beam theory!
Comments in the code indicated that is was a modified version of software written by Dr Rodney Entwistle. So I looked up the Entwistle paper too, which is cited below along with a web link. This paper provided some excellent background and context for the Zhao paper.
I started by copying the Matlab functions from the PDF file of the Zhao thesis to discrete files. To confirm that I had copied the code correctly, my first task was to verify that I could repeat the results from the paper. The following is a code snippet that was modified from code in appendix G.1 of the paper. It demonstrates the convergent nature of the algorithm. It takes as arguments the target frequency (300 Hz), the desired ratios for the 2nd and 3rd partials (4.0 and 9.8), the undercut functional form (cubic) and a seed for the iterative algorithm. Here is the run and the program output (captured in Matlab comments).
bar_props.E = 17.96E9;
bar_props.G = 6.75E9;
bar_props.rho = 837.187565;
bar_props.width = 0.06;
bar_props.d0 = 0.01915;
bar_props.bar_length = 0.3;
close all;
[test_coeffs{1},test_reqs{1}]=main('ploton',true,'bar_props',bar_props,'selected_frequency',300,'overtone_ratios',[4;9.8],'profile','cubic', 'coeffs',[6;0.3;0.003]);
%E=1.796e+10 G=6.750e+09 rho=837.2 width=0.06000 d0=0.01915 length=0.30000 profile=cubic
%seed_coeffs = [6.000000000000; 0.300000000000; 0.003000000000]
%=== Loop number: 1
% freq_new = [129.86691; 4.53455; 12.17812]
% freq_new = [129.86691; 4.53455; 12.17812]
% freq_new = [129.86705; 4.53455; 12.17811]
% delta freq = [170.13310; -0.53455; -2.37811]
%=== Loop number: 2
% freq_new = [319.67484; 4.13737; 10.36343]
% freq_new = [319.67484; 4.13737; 10.36343]
% freq_new = [319.67518; 4.13737; 10.36342]
% delta freq = [-19.67482; -0.13737; -0.56343]
%=== Loop number: 3
% freq_new = [299.01530; 3.97747; 9.66143]
% freq_new = [299.01530; 3.97747; 9.66143]
% freq_new = [299.01562; 3.97746; 9.66142]
% delta freq = [0.98471; 0.02253; 0.13857]
%=== Loop number: 4
% freq_new = [299.96624; 3.99930; 9.79651]
% freq_new = [299.96623; 3.99930; 9.79651]
% freq_new = [299.96656; 3.99930; 9.79650]
% delta freq = [0.03378; 0.00070; 0.00349]
%=== Loop number: 5
% freq_new = [299.99992; 4.00000; 9.80000]
% freq_new = [299.99992; 4.00000; 9.80000]
% freq_new = [300.00024; 4.00000; 9.80000]
% delta freq = [0.00009; -0.00000; -0.00000]
%final freqs = [299.99991; 4.00000; 9.80000]
%coeffs = [10.308557568566; 0.322686204614; 0.006247284721]
In the highlighted line at the end, you can see that the algorithm converged to the desired final frequency and ratios in just a handful of iterations. It also provided the coefficients to the cubic that provided the desired overtones.
The graphical output from this run is at the top of this post. The two figures show the computed bar shape with the bar lying upside down (i.e., with the undercut at the top of the plot). The top figure has an aspect ration of 1:1, and the bottom figure zooms the y axis to better show the curve shape. There are multiple profile because the figure redraws the computed profile after each iteration of the converging algorithm. The line corresponding to the most broad undercut came from the final iteration of the code.
This was pretty exciting! I finally had working code that could predict modal frequencies as a function of a specified bar shape.
Using the Code To Design My Bars
As previously stated, I had decided to design my bars to conform to the “double minimum” shape that I had observed on most of the commercial xylophones. To gain experience, I set out with the following plan in mind:
- Use the software to design a “double-minimum” bar.
- Fabricate a “test bar” out of some inexpensive wood (i.e., not Rosewood) that conformed to the computed shape.
- Measure the frequency modes of the test bar to evaluate the accuracy of the predictions.
Step 1 – Designing My Test Bar
I chose a cubic function for the undercut profile. The choice was motivated by the fact that the cubic profile could realize the desired double-minimum shape, but the parabola would have limited the shape to a simple arch shape. The math that computes the bar shape required information about the material type. The code needs the following parameters:
- Young’s modulus (E) – This is also sometimes called the “bulk modulus” and can be thought of as the stiffness of the wood.
- The shear modulus (G) – This is harder to describe, but I found a good description here. To quote “the shear modulus is harder to talk about, but easiest to demonstrate: take a thick stack of paper (like a phone book) and with your hand on the top, push horizontally. The layers of the stack will shear and the top of the stack will move while the bottom stays put. All objects can be thought of as layers of material. How easily will these layers separate from each other? The shear modulus relates how the top layer of a material will move in relation to the bottom layer.”
- The density (rho) – This is just the mass divided by the volume of the material
I measured the density directly, by measuring a prismatic section of the wood and weighing it. I computed the density as 650 kg/m^3.
The moduli were harder to come by. I found the following reference in the Orduna-Bustamante paper previously cited: “N . E. Molin, L-E. Lindgren, and E. V. Jansson, ‘Parameters of violin plates and their influence on the plate modes,’J . Acoust.S oc.A m. 83,
281-291 (1988). Ratios of Young’s modulus in the longitudinal direction to the shear modulus are reported as E/G=22.1 for spruce wood and E/G = 6.9 for maple wood.”
OK, so given Young’s modulus, I could compute the shear modulus. I found a value of E=12.6 GPa here. I found a second reference here that gave E=12.6 Gpa. So I split the difference and set E=12.5 Gpa.
The algorithm to compute the bar profile needs a “seed” to start its iteration. I used a photograph of the Yamaha bar to compute coefficients of a cubic that approximated the bar shape. However, there was a snafu; the algorithm failed to converge to a solution. It uses a fairly basic Newton-Raphson method of minimization to approach the solution. I am not sure why, but this had some problems. I could have probably worked out why this was the case, but I rather chose to use a Matlab minimizer called fmincon that I was familiar with. An advantage of this minimizer is that you can set constraints on the minimization, like disallowing solutions that yield a bar that is too thin. With the code modified to use fmincon, the algorithm converged! Here is the code that I ran:
%20150207 - Design for longest bar (made of Maple)
%Properies from PPT file (Maple Wood Properties)
wood_props.E = 12.5e+9; %
wood_props.G = wood_props.E/6.9; %
wood_props.rho = 650;
wood_props.nu=(wood_props.E/(2*wood_props.G))-1; %Poisson's ratio
load('results_dir/20150201_AllResults.mat','AllResults');
bar_num=1;
results=AllResults{bar_num};
Comment='Bar #01 (Maple)';
bp=results.inputs.bar_props;
bp.E=wood_props.E;
bp.G=wood_props.G;
bp.rho=wood_props.rho;
bp.nu=wood_props.nu;
num_elements=300;
close all
[coeffs,freqs,inputs,opt_results]=main('ploton',true,'bar_props',bp,'selected_frequency',bp.frequency, 'coeffs',results.coeffs, ...
'number_of_elements',num_elements, 'opt_method', results.inputs.opt_method,'lb',results.inputs.lb,'ub',results.inputs.ub,'weights',results.inputs.weights);
%delta freq = [0.00016; -0.00005; -1.51121
%final freqs = [350.81548; 3.00005; 7.51121
%coeffs = [40.559582736574; -3.643168079495; 0.015502032584]
The highlighted line shows that the algorithm gave frequency ratios for the overtones of 3.00005 and 7.51121. The first overtone was dead on, but the second overtone failed to achieve the desired ratio of 6. I tried many variations of the minimizer, but could not coerce it to yield the desired value of r3 (shorthand for the ratio of the third partial to the fundamental). I don’t know why this is the case. Perhaps it is not possible to yield the desired overtone ratio with a cubic function. In any case, as previously stated, I decided to forgo tuning the third overtone, so I didn’t work this problem further.
Here is a figure illustrating the shape of the resulting bar.
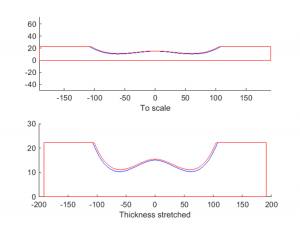
The red profile in this bar corresponds to Maple. The blue profile was computed using the properties of Rosewood. I plotted both to assess the difference between the two materials.
Yee-haw! This seems kind of reasonable. Next step – make the bar out of wood. You’ll hear more about that in the next post (if anyone is still with me…).
References
Entwistle, R.D. and McGrechan, S.R. 2007. Geometric Shape Identification for Multi-Mode Tuning of Percussion Instrument Bars. Proceedings of the 14th International Congress on Sound and Vibration. Cairns, Australia, 9-12 July 2007.
Zhao, Mingming. 2011. “Automatic multi-modal tuning of idiophone bars,” Masters Thesis, M.Phil. Curtin University, School of Civil
and Mechanical Engineering, Department of Mechanical Engineering
Stone, B. 1992. “The receptances of beams, in closed form, including the effects of shear and rotary inertia,” Journal of Mechanical Engineering Science 206 (2): 87-94.

Hello!
I have read with great pleasure your self-construction description of the xylophone. I myself am about to plunge into a similar project: the construction of a marimba. It was of course nice to find sites like yours on the net, which deepened with such enormous detail in the topic. At this point a small warning: I have translated this German-written text by Googles Translator, please do not be surprised if one or the other passage sounds funny. Why I write you is my attempt to get the calculation of Zhao and Entwistle running in Matlab. Unfortunately, I am still not familiar with this program at all, and the debugging does not work well, I keep coming back to places where it does not go any further. I turn around so pretty silly in the circle, and find no approach to the matter to run. I’m probably not a good mathematician either. My question to you is: Would you be so kind as to provide me with your program codes by email once? That would be tremendously helpful, perhaps I would then there again “some land see”. In addition, I would also like to know what values you have entered for the Padouk bars when you were satisfied with the trials with the wood type Maple.
First of all, thank you very much for your effort and a big compliment to the construction of your xylophone. I wish you and your son a lot of pleasure.
Hi Martin – I’ve been very busy lately, so haven’t had a chance to find the code. I will try to find it this weekend and will get it posted. I am not sure about the material properties of Padouk, as I used Rosewood for my bars. I seem to recall I found some data on Padouk and probably annotated it in the code. The Maple bar that I constructed had the correct tonal characteristics but had very poor sustain (the sound died out very quickly), so it is unsuitable for an actual instrument.
Glad the website was helpful. Best of luck with your project!
Rich
Hi Rich, thank you very much for your comment. I am very excited to see if you will have the opportunity to search the program listing for me. In my version, which I from the PDF of Mr. Zhao typed, I unfortunately come during the run to different error messages, which I unfortunately could not interpret correctly. In addition, I have found that it makes a difference whether the coeffs a1 = 6, a2 = 0.3 and a3 = 0.003 are used for each new bar, or, as you have described, the new coeffs for the subsequent one Calculation of the next bar. But at the latest note C5 the program remains stuck, because it wants to run no more calculation. All in all, I come to the conclusion that somewhere a fat error has settled, and which I unfortunately can not recognize. The more I am looking forward to your program listing and hope to get the calculation better under control. Many thanks in advance! Martin
So sorry Martin – I totally spaced this. I have pasted all of the code in my latest post. As stated in the post, this code is kind of messy, but perhaps it will help you to find your error. At a minimum, the COMMANDS.m file contains example runs that you may be able to use to verify my results. One caveat is that I used the optimization toolbox for many of my runs because I had trouble with getting the Zhao code to converge in some cases. If you don’t have that toolbox you may not be able to replicate some of my results. Best of luck – please let me know how your work proceeds.
My wife is a retired elementary music teacher. she still does volunteer work and we buy used xylophones when we can. We bought a Stagg xylophone that could use some improvement. I want to add resonator tubes. I searched your site but don’t really see the process for making these. I want to use PVC. Do you have anything to share?
Hey Jerry –
It’s been a few years, so don’t know if you care any more :-), but chapters 22 and 23 discuss the tube fabrication. As noted in the blog, the hard part was the design of the moveable stoppers. These days I have a 3D printer, so I would probably just print stoppers!
Best, Rich
Wow great job! Thanks so much! But something botter me: you droite about thé density in km per cube meter, dont you mean kg per cube meter?
Thanks Matthieu! Did I mess say km/m^3? I will see if I can find that and fix it. Sorry about the error!
Best, Rich