In the last post, Jack and I turned all of our blanks into shaped bars by cutting and sanding a bit proud of the computer-generated profile line. Now we had to “rough tune” them in preparation for drilling the suspension holes. I had previously noted that drilling the holes had almost no effect on the frequencies for our maple test bar. However, I did a quick test on a much shorter bar and found a significant “flattening” of the fundamental mode. We decided to rough tune each of the bars to about 50 cents sharp to pre-compensate for the hole drilling.

Temperature and Humidity

In our correspondence, Dr Entwistle and I speculated about the affect of temperature and moister content on the sonic properties of the bars. Rodney suggested that perhaps friction heating resulting from the drum sander might affect the spectral measurement. This was a good point, so I decided to do a quick temperature sensitivity experiment.

First, I took one of my prismatic Rosewood bars and measured the spectral characteristics at room temperature to establish a baseline. The fundamental was at 1868.0 Hz at a thermal equilibrium temperature  of 18.1 C. I let it soak in the fridge overnight, and measured the cold temperature at 1.0 C. I then removed the bar from the fridge and quickly measured the fundamental to be 1884.8 Hz. I was surprised that the frequency didn’t change more. This is only about a 0.9% change (15 cents) for a 17 deg decrease or about 1 cent/deg. This result was good news, because it suggested that I did not have to worry too much about bar heating during the tuning process.

Moisture content was a different story. The process of developing the tuning process, and the mechanics of tuning 44 bars took months. I purchased the Rosewood in January of 2015, and finished the tuning in October – about 10 months. During this period, I noticed a consistent pattern; whenever I left weeks or months between spectral measurements, I would notice a significant sharpening of the bar frequencies. I suspected that this was due to wood dry-out over time. You may recall me noting that the vendor who provided the wood stated that he had recently received the shipment of Honduras Rosewood – it had not been in Albuquerque long prior to my purchase. I can only speculate where the wood came from, but it is likely that it was from a climate that was more humid than the arid desert of Albuquerque. New Mexico has a typical relative humidity that is typically 10 or 20%, so we are more dry than just about anywhere.

When I first got my Rosewood in January, I measured the density of a couple of prismatic test bars. To establish the density, I weighed the bars and accurately measured the dimensions. This yielded the following densities.

January 2015
rho1 = 1081.7 kg/m^3
rho2 = 1082.1 kg/m^3

Just today I re-weighed the bars and re-calculated the densities as

February 2016
rho1 = 1042.4 kg/m^3
rho2 = 1041.9 kg/m^3

This is about a 4% decrease in density over 13 months. Wow! This will certainly have an affect on the bar frequencies.

I guess the lesson is that one should properly season the wood to their local climate prior to tuning these bars. (Anectodally, Dr Entwistle suggested letting the bars acclimate for a year or so prior to shaping them, but I was just too eager to get to cutting!) In any case, I lucked out in that the bars got sharper, rather than flatter over time. Recall that it is much easier to decrease the modal frequencies than it is to increase them. This would have been a serious mistake if I lived in a more humid climate, such as Florida. This is another big “lesson learned” for those of you out there who may be attempting to build your own instruments.

Back to Tuning…

First, we re-cut the three bars that were sonic outliers. This was not a big deal, but did involve all of the familiar steps (ripping, planing, jointing, sanding, etc.). It’s so much faster the first time when you are doing it in volume! We also printed new labels and got them adhered to the bars. The frequency response on these new “blanks” was in family with the bars around them, so we were comfortable moving forward with shaping.

In our first run at tuning, we got 20 done. We were shooting for about 50 cents sharp on both the fundamental and first partial. The graph below shows the current state of our first 20 bars.

As you can see, the first and second partials are well behaved for most of the bars. The third partial, which we decided not to tune, wanders around similarly to other xylophones that we had  spectrally measured.

Note that as the bars got shorter, the computer-generated bar shape became less accurate. As you can see on bar 16, 18 and 20, the second partial is tuned about perfectly (not 50 cents sharp, as targeted). This is not due to my tuning, but rather because the second partials for these bars were already closely tuned directly after band-sawing the shapes ~2 mm proud of the computed profile. To tune these bars, I removed wood only at the center of the bar to minimize the affect on the second partial. As you can see in the following photo, these bars shapes have deviated quite a bit from the computer prediction.

Over the subsequent weekend, Jack and I were able to get the rest of the bars tuned. Here are the tuning results:

The fundamental on all bars was pretty good except for bar 29 (my A6 bar,) on which I must have daydreamed while sanding, thus making it a bit flat. I thought that I might need to fix that bar, but that turned not to be the case since the moisture dry-out sufficiently sharpened the bar prior to fine tuning. The second partials above bar 21 (C6) were mostly flat even with the +2 mm rough sawing. However, I was not concerned, because this is consistent with other xylophones that I measured. For example, here is the tuning for the Kori xylophone  that I measured:

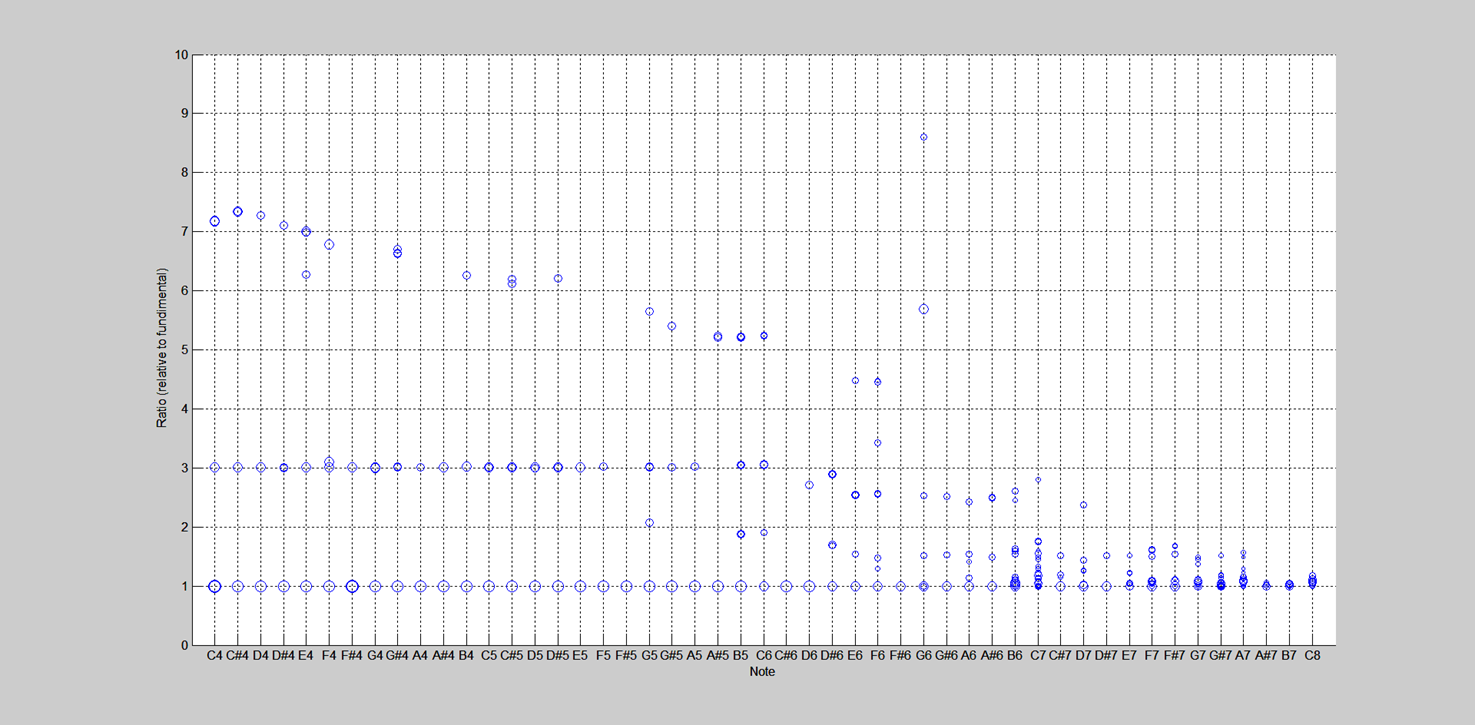
As you can see, for the bars above C6 the second partials for this xylophone are whacky or too quiet to measure.

Here are photos of all of the bars, rough tuned:

The photos show that, starting at bar 18, I had to cut a very narrow notch at the center to yield the desired tuning. As noted above, this is because the rough-sawed shape already had a second partial that was close to the +50 cents desired. As I’ve said previously, the computer predictions start to break down for the shorter bars (as a point of reference, bar #18 is about 11.5 inches long). I don’t think that this is due to inconsistency with a single bar, because the issue seems systematic for all of the “shorter” bars.

Another limitation that I found with the computer results concerns the tuning curves. For example, here is the tuning curve for bar 21:

This curve shows a subtle sharping of the 2nd partial for wood removed at the center. The trend gets more pronounced for the shorter bars. However, I saw no evidence of this when removing wood at the center. I typically saw no change in the second partial with wood removed from the center. As I’ve discussed previously, all of this is likely just a limitation in the approach (i.e., bar theory).

An Improvement?

Later, after doing all of the rough tuning, it occurred to me that I could have modestly improved on my approach to the computer predictions. Specifically, since I performed frequency measurements for each of the Rosewood blanks, I could have used these to compute the modulus for each bar. I could have used this, plus the measured densities for each bar to compute the bar shape for each bar’s paper template. (Recall that I used a single average modulus value and density for all bars.) While I am guessing that this would have reduced variability between the predicted and measured bars, I doubt that it would have significantly improved the systematic issues I saw with the short bars which are most likely the result of the “plate-like” geometry of the shorter bars. Nevertheless, using the per-bar modulus and density seems like a better approach and one that I would recommend.

Wrapping Up the Rough Tuning

Because the computer predictions only approximate the nodal locations for bar, Jack and I used the “salt method” to determine the actual node locations. Here are a few photos. First, is a photo of the salt results for a long bar, including the pencil marks I drew through the salt “mounds.”

Here is one of the shorter bars, before and after strikes with the mallet:

The salt results for bar #40 were curious – the nodes did not form lines at all, but rather fairly circular clusters as shown here:

This one also had an atypical spectrum, as shown here:

The zoomed plot shows that there were two modes that were very close together.  Compare this to bar #39, which was typical of the spectrum for most of the short bars.

Bar #39 shows a nice, single discrete fundamental mode.

Dr Entwistle suggested that perhaps the two close modes that were were observing with bar #40 was the result of a torsional mode closely coinciding with a bending mode. We spent a bit of time trying to ring up the torsional modes to test this theory, but found it difficult. The La Favre site showed some torsional mode results, but that was for marimba bars which are substantially wider.

Bar #40 definitely seemed like an outlier. It also sounded a little different than the others – perhaps a little less “bright” than its neighbors. Jack and I considered remaking this bar, but in the end, decided that it wasn’t worth the effort, given the subtle effect.

The Sound

Here is a sound file containing all of the rough-tuned bars:

A few notes on this sound file:

1. The mallet double-bounced on some of the strikes, which you can hear.
2. You can hear a “warbling” for the first few bars. This is due to the Doppler effect that result from the bar bouncing on the rubber-bands of the tuning jig after the bar is struck. As an aside, this warble is perhaps a few Hz so I later wondered if it could be broadening my spectral peaks and reducing the accuracy of my spectral measurements. A modification of the tuning jig that utilized e.g., felt strips rather than rubber bands would have addressed this potential issue.
3. You may also be able to hear the flat A6 bar.

Having rough-tuned all of the bars, I guess if I were going to do this again I might do some sanity checks along the way to identify anomalous bars early to avoid unnecessary work. For example, after cutting each bar to length, but prior to sanding, attaching the label, or rough-cutting the under-shape, I would probably do a quick spectral check and do the salt method. Then, I could reject any bars that were out of family with the rest. For example, I would check for:

1. A fundamental or second partial out of family with the rest
2. The double peak in the fundamental (like my bar #40)
3. Out of family salt results (i.e., weird nodes)

This quick up-front work could save some considerable re-work down the line.

As a teaser, here is a photo of our 44 bars in an approximate lay out. Pretty cool to see it becoming an instrument!