As the previous posts note, the desired frequency ratios for the first 3 partials of a xylophone are 1:3:6.  However, I needed to know how accurate these frequencies had to be to yield a nice-sounding instrument. I couldn’t find comments on the web about the tuning accuracy requirements, so I set out to spectrally measure some instruments to serve as a guidepost. Specifically, I needed to know how accurate I needed to tune the fundamental and higher partials.

Finding Sound Samples On the Web

The web was pretty skimpy when it came finding sound clips of xylophones.

Here was the first clip that I found – basically a guy playing a C-major scale. There was no info on the type of xylophone he was playing, but it looked pretty decent.

Here is another video that I found of a DeMarrow instrument. He hits some notes at the end of the video.

Finally, at  this site I found a third clip of a guy from the Oregon Symphony playing an xylophone. Again, the I couldn’t find the xylophone brand, but decided it must be a good one if it is used in the symphony.

Spectral Analysis

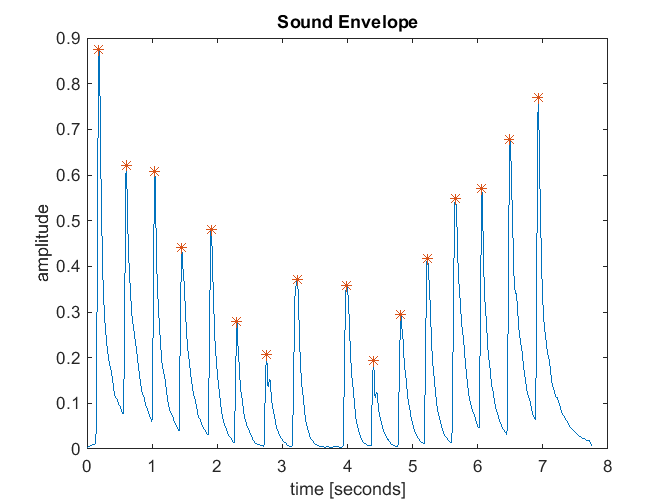
So here is where the magic starts – I wrote some software in Matlab that analyzes these clips to determine how accurately tuned the xylophone is. The tool, called AnalyzeClip, performs the following steps:

1. Read the WAV file.
2. Delineate  each discrete note (i.e., each time a bar is struck) into its own clip.
3. For each clip, perform a windowed spectral analysis.
4. Find the peaks in the spectrum (aka, the modes). This identifies the frequencies associated with the fundamental frequency and the higher partials.
5. Find the fundamental. This is the lowest mode and typically has the most power (although not always – sometimes I found that the second partial had more power.)
6. Associate the fundamental with the closest ideal note, assuming an equal-tempered scale with a 442 Hz reference pitch (Wikipedia has a nice description of equal temperament.)
7. Compute the frequency error of the fundamental relative to the ideal desired pitch.

The “ideal pitch” noted in the last step is computed for a an equal tempered scale with a 442 Hz reference. The notes in an equal tempered scale have a ratio that is given by 2^(1/12) power, which is about 1.0595. So if you want to determine the frequencies associated with a note, just multiple the previous notes frequency by 1.0595. If you do this multiplication for 12 successive notes, the two bookending notes will have a ration of 2, or an octave apart. For my 3.5 octave xylophone, the following table gives the desired frequency for each note.

Note frequencies

Bar Number	Note	Frequency
1	F4	350.816
2	F#4	371.676
3	G4	393.777
4	G#4	417.192
5	A4	442.000
6	A#4	468.283
7	B4	496.128
8	C5	525.630
9	C#5	556.885
10	D5	589.999
11	D#5	625.082
12	E5	662.252
13	F5	701.631
14	F#5	743.352
15	G5	787.554
16	G#5	834.385
17	A5	884.000
18	A#5	936.565
19	B5	992.256
20	C6	1051.259
21	C#6	1113.770
22	D6	1179.998
23	D#6	1250.165
24	E6	1324.503
25	F6	1403.263
26	F#6	1486.705
27	G6	1575.109
28	G#6	1668.770
29	A6	1768.000
30	A#6	1873.131
31	B6	1984.513
32	C7	2102.518
33	C#7	2227.540
34	D7	2359.997
35	D#7	2500.330
36	E7	2649.007
37	F7	2806.525
38	F#7	2973.410
39	G7	3150.218
40	G#7	3337.540
41	A7	3536.000
42	A#7	3746.262
43	B7	3969.026
44	C8	4205.036

Notice that bar 5 (A4) has a pitch of exactly 442.00 Hz. This is because I referenced all of the other notes to this pitch.

In my next post, I will show some results form the spectral analysis of the sound bites that I found on the web.

Having never played a xylophone (or even seen one up close) I decided my first step was to check some out – first on the web, and the up close and personal.

Typical Characteristics of Commercial Instruments

I found a lot of pictures on the web of commercial instruments made by Musser, Malletech, Deagan, Yamaha, etc. that I used to sort of check out the least common denominators. Most concert instruments were 3.5 octaves, which means they had 44 bars that typically spanned the range F4-C8. This range seemed to be most common, so I decided to use it to baseline my design. I also discovered that that there are basically two tunings: The A4 bar can either be tuned to a frequency of 440 Hz or 442 Hz. The literature suggested that 442 tended to sound brighter with an orchestra and is more common, so I decided to tune mine to that frequency.

Bar Materials

I also saw that there were at least three bar materials that were common. The first is a synthetic called Kelon. I’m not sure exactly what Kelon is, but it kind of feels like fiberglass. The advantage of Kelon is that it is cost effective and doesn’t change tune with humidity and temperature. Here’s a link to a pretty nice Musser xylo made of Kelon.  Through my research, it appeared that Kelon is primarily used for instruments that see a lot of travel and abuse (e.g. schools).

I also saw a lot of instruments made of an exotic hardwood called Padauk. Here is a link to a Yamaha xylophone made of Padauk. It appeared that instruments made of Padauk were more expensive than those with Kelon, yet less expensive than those built with Honduras Rosewood, which is the traditional wood used to build xylophones and marimbas.

Ah Honduras Rosewood…the holy grail of xylophone woods (cue angel chorus and sunbeams). As you move up the xylophone food chain, pretty much all of the high-quality instruments are made of Honduras Rosewood. It turns out that this wood is unique in its properties relative to making idiophones (Remember? Instruments that you whack.) If you check out the paper by Aramaki cited below, you can see that they build bars from 59 species of wood. Which one came out on top? You guessed it, Honduras Rosewood.

Dimensions

OK, so after a little research, I had settled on a note range, a tuning pitch, and a  bar material. The only basic characteristic left to decide  was size. If you troll around the web, you can see that bar sizes vary quite a bit. For example, from the LaFavre site, I found the dimensions of the F4 bar (the longest bar) on a Deagan was 12.81 x 1.93 x 0.95 inches. However, the F4 from a the Kori instrument I measured was almost 17 inches long. These tended to be the extremes I found, and most other instruments had bar lengths within this range. As we will see later, a wide range of bar lengths can be shaped to yield the desired frequencies. From a physics standpoint, the larger bars will produce more more volume, as they have more surface area that is creating sound. However, this greater amplitude comes at the expense of compactness and portability.

In the end, I modeled the dimensions of my instrument off of a rosewood Yamaha instrument that seemed to be popular. The specific instrument is a Yamaha YX-500R and can be found at this site.  I liked the overall dimensions of the Yamaha, as my instrument has to fit in my house. Best of all, I was able to find a exploded diagram with parts list on the Yamaha site! Here is one of the diagrams.

and here is a section of the parts list.

The bar description has the length and width of the bars. Sweet! The longest bar on this instrument is 380 x 38 mm which is about 15 x 1.5 inches, which is right in the middle of the range of most of the xylos I found. Also, by following the dimensions of the Yamaha instrument, I was able to ensure that I would build a xylophone that was 1) about the size expected by a musician and 2) had bar lengths that were guaranteed to be tunable.

Next Up

In this discussion, I focused mostly on the physical attributes of the commercial instruments that I found. In my next post I will dig in to the sound characteristics, including more than you probably want to hear about the spectral analysis software I wrote, and the results from a few instruments I analyzed.

References

Aramaki et al. 2007: Aramaki, M., Baille`res, H.,Brancheriau, L., Kronland-Martinet, R., and Ystad, S.(2007). “Sound quality assessment of wood for xylophone bars”, J. Acoust. Soc. Am. 121, 2407–2421.